Una nuova scienza del misticismo: Pitagora ai giorni nostri

 Pitagora fu il padre della scienza e del misticismo occidentali. La sua figura storica è avvolta nella leggenda – era considerato un dio e si diceva che operasse miracoli – ed esistono molti punti oscuri riguardo la sua vita e i suoi insegnamenti. Persino le date di nascita e di morte sono incerte (forse il 569 e il 470 a.C.).
Pitagora fu il padre della scienza e del misticismo occidentali. La sua figura storica è avvolta nella leggenda – era considerato un dio e si diceva che operasse miracoli – ed esistono molti punti oscuri riguardo la sua vita e i suoi insegnamenti. Persino le date di nascita e di morte sono incerte (forse il 569 e il 470 a.C.).
Conosciamo il suo pensiero grazie ai molti seguaci, inclusi Platone e Plotino, e gli antichi biografi Porfirio, Giamblico e Diogene Laertio. È pressoché certo che sia stato allievo dei filosofi greci contemporanei e che abbia soggiornato per lunghi periodi in Egitto e Babilonia. Mentre era in vita, i suoi insegnamenti vennero tenuti in gran parte segreti, ma non ci sono dubbi sul fatto che Pitagora stesso fosse una persona straordinaria. Comunque, tutto ciò che gli viene attribuito è inevitabilmente di origine dubbia, ed è possibile che molto di ciò che insegnò derivasse da fonti più antiche.
Cosa avrebbe pensato Pitagora delle nostre moderne idee sul mondo? Immaginiamo che una macchina del tempo lo abbia trasportato ai giorni nostri e che egli abbia studiato gli sviluppi della matematica, della musica, della filosofia e della fisica negli ultimi 2500 anni. Ora abbiamo avuto l’opportunità di intervistarlo.
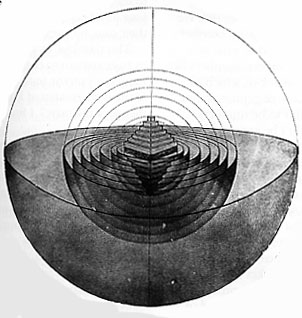
Figura 1 Sistema babilonese dell’universo.
Christian Wertenbaker: Ebbene, trovi congeniale la nostra civiltà moderna?
Pitagora: Naturalmente, le vostre invenzioni tecnologiche sono assolutamente fenomenali e alcune sono davvero meravigliose. Inoltre avete sviluppato, almeno in alcuni luoghi, le idee di democrazia e di diritti umani nate nel mio Paese più di duemila anni fa. Ma la vostra vita è così febbrile! Che fine ha fatto il diritto di contemplare un’idea per lungo tempo o di avere una conversazione senza interruzioni? Ma non ci siamo incontrati per parlare di queste cose; volevi farmi delle domande sulle mie idee scientifiche e matematiche, e se al giorno d’oggi esse conservano un senso.
Christian Wertenbaker: Hai ragione. Suppongo che la prima domanda sia: com’è cambiata la natura dell’indagine scientifica e matematica dall’epoca dei tuoi fondamentali contributi?
Pitagora: Affrontiamo le due cose separatamente, anche se sono chiaramente collegate. In tal modo, possiamo anche parlare di ciò che non è cambiato, che secondo me è la parte più interessante. Innanzitutto, il cambiamento maggiore nella scienza è riportato in tutti i vostri libri di testo: la chiarificazione e la fedeltà a quello che chiamate il metodo scientifico, secondo il quale tutto deve essere verificato sperimentalmente; la speculazione e la logica non sono sufficienti. Naturalmente, io condussi esperimenti su corde vibranti e altri corpi, e facemmo osservazioni attente dei moti planetari, ma all’epoca gli esperimenti non erano considerati importanti. Inoltre, non disponevamo dei sofisticati mezzi di misurazione che avete inventato, come il microscopio, il telescopio, gli acceleratori di particelle e così via. Anche la precisione della logica è aumentata, soprattutto grazie all’opera dei matematici. Quindi, tutto è più rigoroso.
D’altra parte, è possibile affermare – come fanno molti contemporanei – che l’anima o il sentimento sono scomparsi dalla scienza. È come il vostro capitalismo moderno: la priorità è fare soldi, e la qualità, la bellezza, l’appagamento e l’empatia sono tutte cose secondarie. In modo simile, nella scienza la produzione di fatti è diventata eminente; lo scopo della vita, il significato della natura, la percezione di una comunione con un universo conscio e vivente, sono scomparsi. Noi consideravamo i numeri principi divini, e ci connettevamo a essi non solo tramite il pensiero, ma anche attraverso un sentimento superiore.
Tuttavia, tale concezione – anche se contiene qualche verità – è in qualche modo superficiale. Molti grandi scienziati della vostra civiltà furono e sono dei mistici, anche se potrebbero non ammetterlo. Newton passò più tempo sull’alchimia che sulla legge di gravità e l’algebra. Einstein fece affermazioni come: “Voglio sapere in che modo Dio ha creato l’universo. Non sono interessato a questo o quel fenomeno. Voglio conoscere i Suoi pensieri, il resto sono dettagli”. E anche: “Il principio creativo risiede nella matematica. Quindi, in un certo senso, ritengo che il pensiero puro può cogliere la realtà, come sognavano gli antichi” (nota 1). Molti matematici e fisici contemporanei pensano, come Einstein, che una teoria matematica non può essere vera se non è anche bellissima.
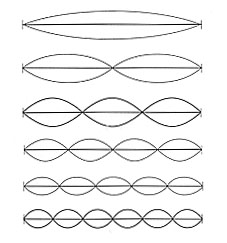
Figura 2 Modelli vibrazionali di una corda.
Christian Wertenbaker: Pensi che oggi l’eccesso di informazioni sia un problema?
Pitagora: Sì, nessuno è più in grado di comprendere nemmeno tutta la matematica, e quest’ultima è così complessa che occorrono anni per cominciare a capirla. Ai miei tempi, una persona intelligente poteva studiare tutto lo scibile. Oggi bisogna fidarsi degli esperti per comprendere il significato di alcune teorie scientifiche, ma gli esperti stessi potrebbero non comprendere tale significato. Nessuno capisce davvero il significato della teoria quantica, anche se sono stati fatti moltissimi sforzi. Per molto tempo – e ancora oggi, in certa misura – tra gli scienziati era prevalsa l’idea che fosse inutile cercare di comprendere il significato di qualcosa: non era questo il compito della scienza. Ma gli esseri umani non possono fare a meno di cercare il significato: è il loro bisogno più insopprimibile. Gran parte della fisica e della teoria matematica moderne contraddicono il senso comune che sviluppiamo vivendo sulla terra. La relatività e la teoria quantica, le pietre angolari della fisica moderna, per noi sono prive di senso. Ma la verità di queste teorie, anche se incomplete, è innegabile, e tutti voi usate felicemente i vostri transistor, CD e impianti di energia nucleare, nessuno dei quali esisterebbe se queste teorie non fossero vere e comprese almeno parzialmente.
Christian Wertenbaker: È interessante il fatto che ora il sapere è accessibile a tutti – qualcuno direbbe che è troppo accessibile, visti gli orrori prodotti dalla scienza – tuttavia resta celato a molti, a causa della sua complessità. Ai tuoi tempi, la conoscenza era tenuta segreta, benché fosse più comprensibile.
Pitagora: Beh, da un certo punto di vista era più comprensibile. Ma, di nuovo, questa analisi è in qualche modo superficiale. Il sapere mistico che è esistito sin dai tempi più antichi è sempre stato contrario, in parte, al senso comune e inaccessibile alla mentalità ordinaria. Non voglio dire che la scienza moderna e il misticismo siano la stessa cosa. I loro metodi sono molto diversi. La scienza considera il sapere, in un certo senso, qualcosa di esterno: esso deve essere dimostrabile tramite manipolazioni del mondo esterno. Per il misticismo, il sapere autentico è raggiungibile dall’interno, grazie a una consapevolezza più elevata, inclusiva ed educata in modo speciale.
Questo presuppone che noi esseri umani possiamo essere in sintonia con l’essenza del cosmo. Per molti scienziati questa è una chimera senza prove, e di certo è possibile dimostrare che le “rivelazioni” di molte persone non sono altro che allucinazioni. Per questo, gli scienziati esigono la verifica esterna. Ma in entrambi i casi è necessaria un’educazione speciale, e se ci pensi bene, anche la fede nella logica e nell’osservazione presuppone una sorta di sintonia con l’universo. Nei miei momenti di maggiore ottimismo, penso che la scienza abbia assunto la forma attuale per rendere più rigoroso il sapere mistico, e che le due forme di conoscenza sono destinate a fondersi.
Christian Wertenbaker: Alcuni ritengono che la teoria quantica sia strettamente collegata alle verità mistiche.
Pitagora: Sì. Nella teoria quantica è il tipo di osservazione a determinare se un elettrone, o qualsiasi altro mattone fondamentale della materia, apparirà come un’onda o una particella. È possibile interpretare questo fatto come una dimostrazione del ruolo ineludibile della consapevolezza all’interno dell’universo. Molti scienziati contestano questa affermazione, ma alcuni tra i più insigni, come von Neumann, sono arrivati esattamente a questa conclusione. Quindi, forse, il risultato finale della vostra scienza moderna sarà la conferma, da un punto di vista diverso, delle grandi e antiche verità mistiche – anche se sicuramente c’è ancora molta strada da fare – e l’eliminazione di alcune delle stupidaggini che sono state promosse nel nome del misticismo. A quest’ultimo proposito, farei a meno di certi guazzabugli sviluppatisi dalle mie stesse idee nel corso dei secoli.
Penso che la differenza autentica tra la scienza moderna e il vero misticismo stia nel fatto che lo scienziato cerca deliberatamente di ignorare il ruolo del soggetto nella comprensione del mondo. Ma nessuna comprensione esiste al di fuori di un essere conscio; essa non esiste sulla carta, nelle formule e nei diagrammi. Inoltre, la scienza non considera l’esistenza di diverse capacità di apprendimento, dovute non solo all’educazione intellettuale, ma anche allo sviluppo (ancora più rigoroso) di una consapevolezza più elevata, che è il fine degli insegnamenti mistici.
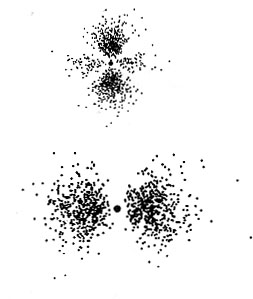
Figura 3 Modelli vibrazionali dell’idrogeno (distribuzioni di probabilità dell’elettrone).
Christian Wertenbaker: Cosa mi dici della matematica? In che modo è cambiata? Come hai detto in precedenza, ora essa è molto più vasta, ma quasi completamente oscura per la maggior parte delle persone.
Pitagora: I mutamenti sono stati enormi, naturalmente. La differenza è la stessa che passa tra una vostra Mercedes e un antico cocchio greco. Il principio fondamentale del trasporto su ruote, comunque, resta lo stesso. Nel caso della matematica, il nostro detto “Tutto è numero” sembra più vero che mai. La sorprendente applicabilità delle strutture matematiche al mondo fisico è stata osservata più volte. Adesso voi avete più tipi di numeri di quanti ne avevamo noi.
A noi non piaceva usare nemmeno i numeri negativi o lo zero, ed eravamo perplessi di fronte a quelli che chiamate numeri irrazionali, come la radice quadrata di due o il pi greco; questi ultimi li conoscevamo grazie alla geometria, ma non li consideravamo numeri veri e propri perché era impossibile esprimerli come proporzioni esatte. Adesso tutti questi tipi di numeri (inclusi i numeri complessi, che implicano la radice quadrata di meno uno) sono entrati a far parte della matematica, con risultati meravigliosi. E poiché sembra che non esistono altri tipi di numeri da scoprire, il processo è terminato.
Una delle scoperte più valide è il calcolo, che rende possibile lo studio di processi in mutamento continuo, come il moto, grazie a un metodo che permette di padroneggiare cambiamenti infinitamente piccoli. Esso risolve alcuni dei paradossi scoperti nella Grecia antica, oggi conosciuti come i paradossi di Zenone. Per esempio, Zenone argomentava che il moto era impossibile, perché per andare dal punto A al punto B, devi necessariamente attraversare un punto C situato tra i primi due, e prima di arrivare a C, devi passare attraverso D, situato tra A e C, e così via, in modo che di fatto è impossibile cominciare. Il calcolo rende possibile lo studio matematico del moto, incluse le onde di moto, che noi avevamo compreso solo dal punto qualitativo.
Christian Wertenbaker: Ma la matematica non si è allontanata da ciò che alcuni considerano le nozioni elementari dell’applicabilità dei numeri interi semplici – uno, due, tre ecc. – al funzionamento dell’universo?
Pitagora: Ah, no! Vedi, essa ha meramente aggiunto a questi delle verità fondamentali. Esistono ancora tre dimensioni dello spazio, almeno alla nostra scala macroscopica, e ciò determina molte cose. È ancora necessario un minimo di due punti per determinare una linea, tre per determinare una figura piana come un triangolo, e quattro per specificare un solido come un tetraedro. Questi quattro numeri (disposti in un triangolo) e la loro somma (dieci) costituivano la nostra sacra “tetraktys”.
Questa “tetraktys”, per inciso, è identica nel suo schema essenziale ai dieci componenti del tensore metrico di Riemann, una parte fondamentale della teoria matematica generale della relatività einsteiniana (nota 2). Trovo questo fatto assolutamente stupefacente.
L’universo è ancora un tutto. La vostra concezione secondo cui all’inizio di ogni cosa vi fu una singolarità esplosa nel Big Bang (avete davvero dei nomi divertenti per le cose) vuol dire che tutto è interconnesso, sebbene nella vostra scienza non esista ancora l’idea che l’universo intero sia animato. Molti processi dipendono dall’interazione di due forze opposte: è questa perpetua tensione dinamica tra gli opposti a creare l’infinita molteplicità dei fenomeni. Esistono la forza e l’inerzia, le cariche positive e negative, il maschile e il femminile. Ma occorre l’interazione di tre forze, o enti, per produrre un evento o un fenomeno: tutte le vostre equazioni più importanti hanno tre termini.
Per esempio: forza = massa per accelerazione; energia = massa per la velocità della luce al quadrato; corrente elettrica = voltaggio diviso resistenza. E se in un’equazione esistono altri termini, spesso si tratta di costanti. Inoltre, esistono tre componenti negli atomi: protoni, neutroni ed elettroni. Vi sono tre quark in un protone o un neutrone, e i quark si presentano in tre “colori” e tre coppie di “sapori”. Esistono tre note in un accordo fondamentale, e la mescola di tre colori primari può formare qualsiasi colore. Abbiamo tre tipi interiori di cognizione: sensazione, emozione e intelletto.
Esistono quattro dimensioni, almeno alla nostra scala: tre riguardano lo spazio, una il tempo. Gli eventi hanno luogo su una scena composta di quattro numeri. Il cinque entra in scena con la sezione o rapporto aureo, che tanto ci interessava. La formula del rapporto aureo è (√5+1)/2, e la sezione aurea si trova nella stella a cinque punte e in altre figure a simmetria pentagonale; inoltre, è collegata ai numeri di Fibonacci. Questi numeri e il rapporto aureo sono visibili soprattutto negli esseri viventi, dalla disposizione delle foglie su un gambo alla forma dei semi di girasole e dei cactus, fino alla spirale delle conchiglie marine (nota 3).
Il DNA, visto da un’estremità, ha una simmetria a dieci lati. Il cinque e il dieci saltano fuori anche nelle moderne teorie del tutto, nel tensore metrico di Riemann e, con dieci dimensioni, nella cosiddetta simmetria SU(5) e in alcune di queste nuove teorie della stringa. La nostra idea che il dieci fosse l’unica base corretta per un sistema numerico potrebbe rivelarsi profondamente vera quando la fisica moderna otterrà un quadro più chiaro di una teoria davvero fondamentale.
Potrei andare avanti con gli altri numeri che ritenevamo importanti, mostrandoti sia la persistente validità delle nostre idee, sia il loro legame con le scoperte moderne. L’idea dei “numeri magici”, numeri interi semplici che spuntano da ogni parte, è più attuale che mai.
In realtà, la moderna fisica quantica può considerarsi, in parte, un ritorno ai numeri semplici. Il paradosso fondamentale della teoria quantica è che gli enti elementari si comportano sia come onde che come particelle, sia come oggetti continui che come oggetti discreti. Ciò è simile al comportamento delle corde vibranti, alle quali dedicai tanti studi. Le corde vibrano con moto ondoso, ma solo nelle note discrete (quella fondamentale e quelle armoniche). Tale moto ondoso è determinato dai vincoli alle estremità della corda, che devono restare ferme. La corda può essere divisa dalle vibrazioni solo in una, due, tre ecc. parti, creando la nota fondamentale, la sua ottava, la quinta sopra questa, l’ottava successiva ecc.
La descrizione degli atomi utilizza lo stesso linguaggio matematico: corpi vibranti con certe armoniche, questa volta tridimensionali.
Ciò crea la vostra tavola periodica degli elementi. Naturalmente, adesso avete più di cento elementi invece della terra, l’acqua, l’aria, il fuoco e l’etere, quelli che noi chiamavamo elementi. Le nostre idee, tuttavia, sono ancora valide come simboli non degli elementi, ma degli stati della materia: solido, liquido, gassoso, plasma ed energia elettromagnetica, oltre a ciò che adesso chiamate il vuoto, che non è vuoto come la parola lascia supporre, bensì brulica di energia. Ma non colpisce il fatto che gli elementi moderni si dividono in gruppi basati sul numero di elettroni orbitali o di modelli vibrazionali? E che le orbite possono avere, rispettivamente, due volte 1, 4, 9 e 16 elettroni, le radici perfette, e che questi numeri a loro volta vengono dai semplici numeri interi che determinano i modelli vibrazionali?
Una cosa è chiara: tutto vibra, è in vibrazione, e la natura fondamentale del mondo è la vibrazione. Per quanto astratte, complicate e poco intuitive diventino le teorie moderne – che siano dieci o ventisei le corde dimensionali in vibrazione, o i gruppi astratti di simmetria – tutte conservano alla base questa verità fondamentale. E le proprietà degli oggetti vibranti sono determinate dai numeri, allo stesso modo delle tonalità musicali.

Figura 4 Pitagora mentre indica i testi antichi.
Christian Wertenbaker: Ma tu pensavi che la scala musicale, le semplici note rappresentate dalle semplici proporzioni:
1, do; 9/8, re; 5/4, mi; 4/3, fa; 3/2, sol; 5/3, la; 15/8, si; 2, do
fossero il modello fondamentale su cui era costruito l’universo. Di certo le cose non sono così semplici, secondo le idee moderne.
Pitagora: No, non lo sono. Ma penso che diventeranno più semplici quando le vostre teorie si svilupperanno. In realtà, non era quella la scala che usavamo. Nella nostra scala alcune note avevano proporzioni diverse, anche se sempre relativamente semplici. Ed è questa difficoltà nel determinare la scala corretta che mette in evidenza alcuni aspetti molto interessanti dell’analogia musicale.
Le moderne teorie matematiche degli aspetti fondamentali della natura si basano sull’idea di simmetria. Una simmetria esiste quando una proprietà di una configurazione di elementi resta la stessa nonostante una manipolazione della configurazione. Per esempio, se ruoto un esagono di un sesto di cerchio, esso ha lo stesso aspetto. Se non ci fosse simmetria, non ci sarebbero ordine, prevedibilità, modelli; non potrebbe succedere o esistere nulla di riconoscibile. Quindi, non esisterebbe nemmeno l’intelligenza. Il progresso più importante nella fisica matematica moderna è stata la generalizzazione dell’idea di simmetria. Il fatto che io non mi trasformo in un alligatore mentre cammino per la sala riflette una simmetria: le leggi dell’universo non mutano da un punto all’altro. Per il tempo, esiste una simmetria simile: io non svanisco da un momento all’altro. Ma tali simmetrie non sono perfette, perché non tutto resta uguale quando cammino per la sala, né da un istante all’altro. Se esistesse la simmetria perfetta, nulla potrebbe succedere o esistere. Ciò viene ora chiamato simmetria spezzata. La simmetria e la simmetria spezzata sembrano alla base dell’organizzazione fondamentale di ogni cosa (nota 4).
Christian Wertenbaker: Mi sembra che tutto ciò faccia riferimento più alla geometria che al numero o alle scale musicali.
Pitagora: Noi consideravamo tutte queste aeree intimamente collegate, e uno degli aspetti meravigliosi della matematica moderna è che anch’essa ha portato insieme molti concetti apparentemente lontani. Di fatto, questo è l’antidoto alla proliferazione delle informazioni di cui stavamo parlando prima.
I numeri possiedono un genere di simmetria. Alcuni sistemi numerali formano quelli che adesso vengono chiamati gruppi matematici, dei quali non starò a illustrare i dettagli. Ma l’idea è che se prendi, per esempio, gli interi positivi (1, 2, 3 ecc.) e applichi a essi un’operazione sommandoli insieme (allo stesso modo in cui applichi un’operazione su un esagono ruotandolo), la somma produce un altro numero intero, non un coniglio. D’altra parte, se dividi due interi, puoi ottenere un altro intero (6/2=3) oppure no (2/3 non è un intero). Ma 2/3 è un numero razionale – è esprimibile come una “ratio”, un rapporto tra numeri interi – quindi hai un gruppo diverso, i numeri razionali, che puoi dividere tra loro e ottenere sempre un numero razionale. Esistono altri requisiti per i gruppi, ma questa è una delle idee principali. Per cui, le cose possono essere classificate in vari gruppi, dotati di varie simmetrie.
Le note della scala musicale, essendo prodotte da vibrazioni che sono rappresentate da rapporti semplici, hanno questo genere di simmetria. Se sali di un quinto (cinque note sulla scala, e 3/2 il numero di vibrazioni) dal Do, ottieni il Sol, mentre se sali di un quarto dal Sol (4/3 il numero di vibrazioni), ottieni un altro Do, un’ottava sopra il primo, perché 3/2 x 4/3 = 12/6 = 2, e l’ottava è due volte il numero di vibrazioni. In generale, se sali di un certo numero di note sulla scala, ottieni un’altra nota nella scala. Ma dopo un po’ c’è un problema, che scoprimmo molto tempo fa. Per esempio, se sali di 12 quinti:
Do, Do#; Sol, Sol#; Re, Re#; La, La#; Mi, Mi# o Fa; Si; Fa#, Do
Ritorni al Do, sette ottave sopra il primo Do. Ma questa nota non è esattamente la stessa della settima ottava, perché (3/2)12 (3/2 moltiplicato se stesso 12 volte) dà 531441/4096 = 129.746, mentre la settima ottava è 27 = 128. Questa differenza, 129.746/128, o 531441/524288 [nota dell’autore: che venne chiamata il comma pitagorico], è ancora un numero razionale, ma certo non un rapporto di numeri piccoli, come le note della scala. Questo problema portò, qualche centinaio di anni fa, al compromesso della vostra musicale temperata. Ma il problema esiste, perché le potenze del 2 e del 3 non coincidono mai esattamente. Quindi, abbiamo un tipo di simmetria imperfetta, risultante semplicemente dalle proprietà del 2 e del 3.
Questa leggera differenza tra il dodicesimo quinto e la settima ottava, se vengono suonate insieme, produce una lieve dissonanza, una tensione che crea un’altra vibrazione. Questa può essere vista come una forza tra le due note. Penso che ciò sia analogo alle forze residuali, risultanti dalla simmetria imperfetta, che creano i diversi livelli di interazione nel mondo. Fammi citare un articolo che ho letto:
“La forza elettromagnetica tiene insieme gli elettroni e i nuclei, dando vita agli atomi. Gli atomi, sebbene siano elettricamente neutri, interagiscono attraverso una forza elettromagnetica residua formando molecole. La forza forte lega i quark formando protoni, neutroni e tutti gli altri adroni, e la residua forza forte tra i protoni e i neutroni è la cosiddetta forza nucleare che li lega a formare i nuclei” (nota 5).
Ebbene, questa è un’analogia, non una diretta corrispondenza. Non dico che abbiamo anticipato i sorprendenti progressi fatti dalla vostra civiltà con la scoperta delle basi matematiche del funzionamento dell’universo. Ma la stupefacente applicabilità della matematica al mondo fisico è oggi ancora più evidente di allora. I numeri semplici e le proporzioni svolgono ancora una parte importante. Può darsi che, con gli sviluppi futuri della scienza, le corrispondenze tra il pensiero antico e moderno diverranno più forti, a questo proposito. Anche adesso, penso che la vostra scienza stia cominciando ad accostarsi alla dimensione dell’ideale, dell’essenza, che è alla base di tutte le cose, anche se quest’ultima non può essere compresa solo grazie alla scienza.

Figura 5 Pitagora come il Maestro della musica.
Christian Wertenbaker: Qual è, secondo te, l’ostacolo maggiore a una comprensione più completa?
Pitagora: Il ruolo della consapevolezza nell’universo deve entrare a fare parte delle vostre teorie. La fisica moderna riconosce il fatto che il tipo di osservazione di un fenomeno determina in modo essenziale – benché ancora misterioso – la manifestazione della realtà stessa. Ma la consapevolezza deve essere inserita esplicitamente nella teoria, e va compresa la relazione tra il mondo interiore degli esseri consci e il mondo esteriore. Gli scienziati del cervello stanno compiendo adesso, per la prima volta, un grande sforzo per comprendere la consapevolezza; forse ciò servirà a comprendere in che modo questi due mondi convivono.
Note
1. Michio Kaku, Hyperspace: A Scientific Odissey through Parallel Universes, Time Warps, and the 10th Dimension (New York: Oxford University Press, 1994).
2. Ibid., p. 41. La descrizione di uno spazio curvo di quattro dimensioni richiede sedici numeri:
G11 G12 G13 G14
G21 G22 G23 G24
G31 G32 G33 G34
G41 G42 G43 G44
dei quali sei sono sovrabbondanti, per cui ne rimangono dieci. Vedi anche Julian Schwinger, Einstein’s Legacy: The Unity of Space and Time (New York: Scientific American Books, Inc., 1986).
3. Esistono molti libri sull’argomento. Vedi, in particolare, H. E. Huntley, The Divine Proportion: A Study in Mathematical Beauty (New York: Dover Publications, Inc., 1970).
4. Vedi Christian Wertenbaker: Nature’s Patterns, “Parabola”, Vol. 24, Numero 1, febbraio 1999.
5. Howard E. Haber e Gordon L. Kane, Is Nature Supersymmetric?, “Scientific American”, giugno 1986, p. 52.
Acquista i libri con Internetbookshop
Julian Schwinger. L’eredità di Einstein. Zanichelli. 1998. ISBN: 8808053407
H. E. Huntley. The Divine Proportion. Dover.1970. ISBN: 0486222543
Originalmente apparso sulla rivista Parabola: The Magazine of Myth and Tradition www.parabola.org
Traduzione di Gagan Daniele Pietrini
Copyright per l’edizione Italiana: Innernet.